🧠💫机器学习与数据挖掘期末复习
什么是机器学习
机器学习包括几个关键词:计算机、经验/数据、模型、性能、预测
机器学习根据以往的经验和数据得到数学模型,并可以对未知数据进行预测,最终达到计算机算法和程序进行优化的目的
基本术语
- 泛化能力:机器学习的目标是让我们的模型能很好地应用于“新样本”,我们称模型适用于未知新样本的能力为泛化能力
- 监督学习:学习由一个输入到输出的映射,成为模型。模型的集合就是假设空间
- 半监督学习:具有少量标注数据,大量未标注数据,利用未标注数据的信息,辅助标注数据进行监督学习
- 主动学习:属于半监督学习的一种。先训练一个初始模型,给没有标签的数据打上伪标签,然后再用伪标签和其他有标签的数据重新训练模型。重复上述过程
- 模型评估和模型选择:
- 训练误差:在训练过程中产生的误差
- 验证误差:在验证集上进行交叉验证选择参数(调参),最终模型在验证集上的误差就是验证误差。
- 测试误差:训练完毕、调参完毕的模型,在新的测试集上的误差,就是测试误差。
- 泛化误差:假如所有的数据来自一个整体,模型在这个整体上的误差,就是泛化误差。通常说来,测试误差的平均值或者说期望就是泛化误差。
综合来说,它们的大小关系为
训练误差 < 验证误差 < 测试误差 ~= 泛化误差
- 损失函数:损失函数通常是针对单个训练样本而言,给定一个模型输出$\hat{y}$和一个真实输出$y$,损失函数衡量它们之间的差距,输出一个实值损失$L=f(y_{i},\hat{y}_{i})$
- 测试数据集准确度:
KNN(K近邻算法)
- 已有一批有标签的数据
- 输入没有标签的数据后,需要对他们进行分类。将新数据的每个特征和已有标签数据计算相似度
- 选取k个相似度最高的样本,分别统计他们的标签出现次数,出现最多的那个分类作为新数据的分类
如何定义相似度指标
- 直线距离(欧氏距离)
- 街区距离(曼哈顿距离)
- 闵可夫斯基距离:$\sum_{i=1}^{k}(\left | x_{i}-y_{i} \right |^{q})^{1-q}$
- 余弦距离
如何确定k值
- 经验:对于n个训练样本,设置k为$\sqrt{n}$
- 实践中会通过交叉验证来确定k值
k折交叉验证:将数据集划分为k等分,一份为测试集,剩余的$k-1$份作为训练集,比如说第一次选取第一个$\frac{1}{k}$作为测试集,一直循环到最后一份,计算k次测试集上的正确率的平均值。
引入特征的重要性
计算相似度的时候将不同特征加权求和
归一化
不同特征指标单位不同,取值范围也不同,对距离的计算带来比较大的影响。使用minmax进行归一化,也就是将数据变成在区间$(0,1)$之间的小数。
$$
\frac{x-min(x)}{max(x)-min(x)}
$$
- 主要是为了数据处理方便提出来的,把数据映射到0~1范围之内处理,更加便捷快速
- 把有量纲表达式变成无量纲表达式,便于不同单位或量级的指标能够进行比较和加权。
归一化是一种简化计算的方式,即将有量纲的表达式,经过变换,化为无量纲的表达式,成为纯量
标准化
在机器学习中,我们可能要处理不同种类的资料,例如,音讯和图片上的像素值,这些资料可能是高维度的,资料标准化后会使每个特征中的数值平均变为0(将每个特征的值都减掉原始资料中该特征的平均)、标准差变为1,这个方法被广泛的使用在许多机器学习算法中(例如:支持向量机、逻辑回归和类神经网络)。
中心化
平均值为0,对标准差无要求
归一化和标准化的区别
归一化是将样本的特征值转换到同一量纲下把数据映射到[0,1]或者[-1, 1]区间内,仅由变量的极值决定,因区间放缩法是归一化的一种。标准化是依照特征矩阵的列处理数据,其通过求z-score的方法,转换为标准正态分布,和整体样本分布相关,每个样本点都能对标准化产生影响。它们的相同点在于都能取消由于量纲不同引起的误差;都是一种线性变换,都是对向量X按照比例压缩再进行平移。
标准化和中心化的区别
标准化是原始分数减去平均数然后除以标准差,中心化是原始分数减去平均数。 所以一般流程为先中心化再标准化。
无量纲
我的理解就是通过某种方法能去掉实际过程中的单位,从而简化计算。
KNN优点
- 很简单,容易实现
- 可以应用于任何分布的情况
- 样本数量很大也能产生好的结果
KNN缺点
- 参数的选择,k值
- 对分类新的样本时间比较长,因为要计算大量的距离
决策树
CLS算法
早期的决策树学习算法,是许多决策树学习算法的基础,他没有规定策略去选择属性
ID3算法
使用信息增益选择测试属性
$$
H(x)=-\sum p_{i}log(p_{i})
$$
$$
G(D,a)=H(D)-\sum_{v=1}^{V}\frac{|D^{v}|}{|D|}log_{2}\frac{|D^{v}|}{|D|}
$$
信息增益倾向于选择取值较多的特征,因此我们对信息增益归一化,引入增益率
也即是C4.5算法
$$
Gain_ratio(D,a)=\frac{Gain(D,a)}{IV(D,a)}
$$
$$
IV(a)=-\sum_{v=1}^{V}\frac{|D^{v}|}{|D|}log_{2}\frac{|D^{v}|}{|D|}
$$
不过还存在的问题变成了倾向于取值数目比较少的属性
ID3算法的优点是:算法的理论清晰,方法简单,学习能力较强。其缺点是:只对比较小的数据集有效,且对噪声比较敏感,当训练数据集加大时,决策树可能会随之改变。
启发式方法
一种启发式方法是结合二者,先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的
CART算法
使用Gini指标进行属性选择
Gini值:反映了从D中随机抽取两个样本,其类别标记不一致的概率,因此Gini指标越小,代表这样分类的效果越好
$$
Gini(D)=\sum_{k=1}^{|\gamma|}\sum_{k’\neq k}p_{k}p_{k’}=1-\sum_{k=1}^{|\gamma|}p_{k}^{2}
$$
$$
Gini_index(D,a)=\sum_{v=1}^{V}\frac{|D^{v}|}{|D|}Gini(D^{v})
$$
对于连续的问题,可以得到回归树:使用平方误差最小化作为衡量指标选择属性。对划分出来的样本集,计算他们的方差,目标是选取划分之后方差最小的划分方法。
决策树过拟合问题
先从数据集中划分出一部分验证集作为评估指标
- 预剪枝:在模型构建过程中对模型进行剪枝
在决策树生成过程中,对每个节点在划分前进行验证集的估计,如果划分节点对泛化能力不带来提升,则停止划分并将当前节点记为叶节点 - 后剪枝:构建完之后再进行剪枝,方法是去掉每个节点,看能否带来泛化能力的提升,如果可以就去掉
连续值的处理
连续属性a在样本集中出现n个不同的取值,我们从小到大排列,对他们进行二分划分为两部分,划分的时候取中间值
集成学习
bagging
bagging是投票式算法,使用bootstrap产生训练集,从D中有放回抽样,分别基于这些训练数据集得到多个基础分类器,最后通过这些分类器得出模型,这些模型同时进行预测,选择得票最多的那个分类
bagging的特点
- 个体学习期之间不存在强依赖关系,具有独立性
- 可以并行生成
- 算法的复杂度低,训练一个bagging集成与直接使用基学习器的复杂度同阶
使用场景
单个模型不稳定,用集成的方法选择最适合的
训练算法
通过对D有放回抽样,得到t个训练集$D_{t}$,使用$D_{t}$进行训练得到模型$M_{t}$。预测的时候使用组合分类器对样本进行分类,T个模型同时预测,并返回多数的表决
随机森林
随机森林的随机性
- 对样本进行有放回的抽样
- 在对每个点划分的时候,随机选择特征进行考虑
- 样本在某个属性有多个特征值的时候,随机划分进一个特征值的分类中
算法
-
用n来表示训练样本的个数,d表示特征数目
-
输入特征数目m,用于确定决策树划分属性个数,其中m应远小于d
-
从n个训练样本中以有放回抽样的方式,取样n次,形成一个训练集
-
对于每一个节点,随机选择m个特征,决策树上每个节点的决定都是基于这些特征确定的,根据这m个特征,计算其最佳的分裂方式
-
从数据集(表)中随机选择k个特征(列),共m个特征(其中k小于等于m)。然后根据这k个特征建立决策树。2. 重复n次,这k个特性经过不同随机组合建立起来n棵决策树(或者是数据的不同随机样本,称为自助法样本)。3. 对每个决策树都传递随机变量来预测结果。存储所有预测的结果(目标),你就可以从n棵决策树中得到n种结果。4. 计算每个预测目标的得票数再选择模式(最常见的目标变量)。换句话说,将得到高票数的预测目标作为随机森林算法的最终预测。
优点:
- 可以用来解决分类和回归问题:随机森林可以同时处理分类和数值特征。
- 抗过拟合能力:通过平均决策树,降低过拟合的风险性。决策树使用贪婪的思想,容易陷入局部最优,随机森林的随机性可以跳出局部最优。
- 只有在半数以上的基分类器出现差错时才会做出错误的预测:随机森林非常稳定,即使数据集中出现了一个新的数据点,整个算法也不会受到过多影响,它只会影响到一颗决策树,很难对所有决策树产生影响。
- 处理高维数据,不用进行特征选择
- 容易做成并行化方法
缺点: - 据观测,如果一些分类/回归问题的训练数据中存在噪音,随机森林中的数据集会出现过拟合的现象。
- 比决策树算法更复杂,计算成本更高。
- 由于其本身的复杂性,它们比其他类似的算法需要更多的时间来训练。
评价指标:分类间隔,对样本A有75%的分类正确,则分类间隔为75-25=50%
袋外错误率:对每⼀棵树来说,都有样本没有被抽样进⼊训练样本中,这些就是袋外样本。对袋外样本
预测的错误率就是袋外错误率。
boosting
Boosting是一种通过组合弱学习器来产生强学习器的通用且有效的方法。本文中我们将重点讲解三种Boosting算法:AdaBoost, RankBoost, Gradient Boosting。AdaBoost是第一个成功的Boosting算法,所以我们先介绍AdaBoost
adaboost
AdaBoost解决了如下两个问题:首先,如何选择一组有不同优缺点的弱学习器,使得它们可以相互弥补不足。其次,如何组合弱学习器的输出以获得整体的更好的决策表现
我自己的理解:
adaboost对每个样本都维护一个权重分布,每个样本都有一个权重值表示它的重要性,在衡量错误率的时候,权重大的样本分类错误贡献了比权重小的更大的错误率。这使得弱分类器要聚焦于这些高权重的样本,引导这些弱学习器学习训练样本的不同部分,我们进行多轮训练,在每一轮训练中都更新权重分布,对那些误分类的样本提高权重,那些上一轮分类准确的就降低权重,这样每一轮弱学习器都有进步。
训练完之后,我们就得到了一组具有不同优缺点的弱学习器,给他们加权使它们的优势组合起来。
bagging和boosting的区别
- 样本选择:
- bagging:训练集有放回抽样,从原始集中选出的各轮训练集是互相独立的
- boosting:每一轮的训练集都一样只是样本在各个弱学习器中的权重发生变化
- 样例权重:
- bagging:每个样本的权重相等
- boosting:根据错误率不断调整样本的权重,聚焦于分类错的样本上
- 预测函数:
- bagging:所有预测函数的权重相等
- boosting:每个弱分类器都有相应的权重,对于分类误差小的分类器会有更大的权重
- 并行计算
- bagging:各个预测函数可以并行生成
- boosting:各个预测函数只能顺序生成,因为后一个模型的权重需要根据上一轮的分类结果
线性模型
线性判别分析LDA
LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括,就是“投影后类内方差最小,类间方差最大”。什么意思呢? 我们要将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。
可能还是有点抽象,我们先看看最简单的情况。假设我们有两类数据 分别为红色和蓝色,如下图所示,这些数据特征是二维的,我们希望将这些数据投影到一维的一条直线,让每一种类别数据的投影点尽可能的接近,而红色和蓝色数据中心之间的距离尽可能的大。
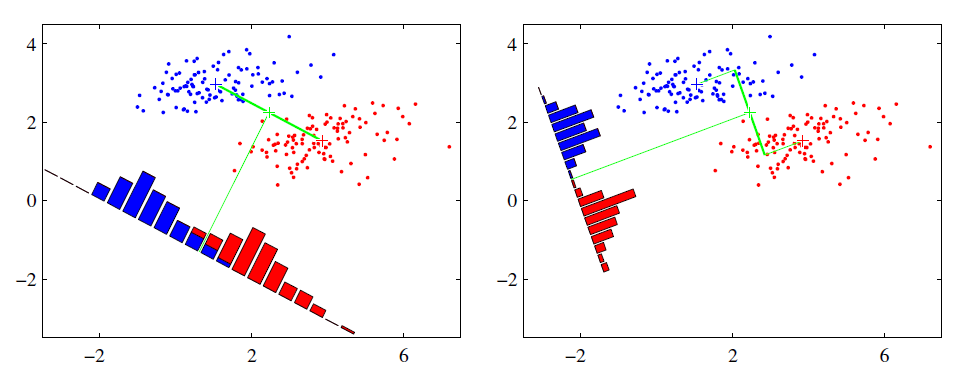
类内散度矩阵
衡量同一类内样本间的距离
$$
S_{w}=\sum_{0}+\sum_{1}=\sum_{x\in X_{0}}(x-\mu_{0})(x-\mu_{0})^{T}+\sum_{x\in X_{1}}(x-\mu_{1})(x-\mu_{1})^{T}
$$
类间散度矩阵
衡量不同类之间的距离
$$
S_{b}=(\mu_{0}-\mu_{1})(\mu_{0}-\mu_{1})^{T}
$$
最大化目标
不同类别间距离最大,也就是投影后的样本他们的均值的方差最大
多分类问题
支持向量机SVM
⽀持向量机的⽬标,是找到⼀个超平⾯,能最好的分隔不同类别的样本。它的优化⽬标是:最⼤化样本
中距离超平⾯最近的距离,约束条件是样本都被正确分隔。也就是:
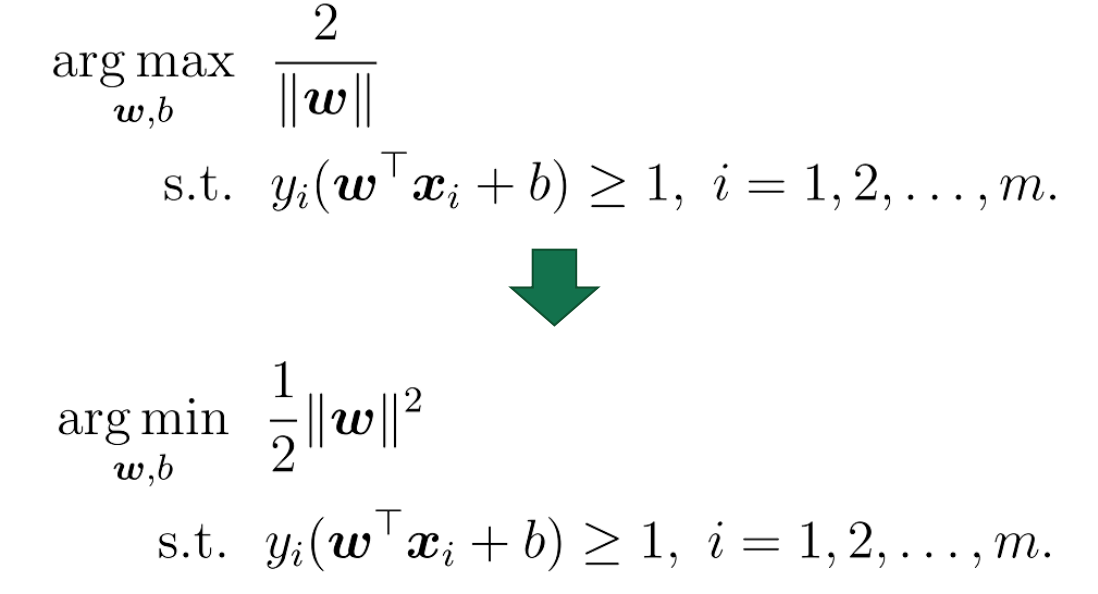
对偶问题
通过拉格朗⽇乘⼦法将原始问题转化为对偶问题,通过解对偶问题得到原始问题的解。
核函数
[随机森林][https://www.zhihu.com/question/64043740/answer/672248748]
